Metoda Elementów Skończonych
W agronomii i agrofizyce metody modelowania numerycznego znalazły szerokie pole zastosowań w rozwiązywaniu zagadnień praktycznych jak i naukowych. Modele tego typu w wielu przypadkach stały się konieczne w zrozumieniu zależności pomiędzy strukturą a właściwościami biomateriałów, takich jak owoce i warzywa.
Wiedza uzyskana dzięki modelom numerycznym oprócz charakteru naukowo – poznawczego jest również użyteczna w praktyce z punktu widzenia zapewnienia jakości owoców i warzyw.
Podstawową ideą metody elementów skończonych (MES) jest podział dziedziny przestrzennej problemu na szereg mniejszych i prostszych pod względem kształtu obszarów. Rozwiązanie ogólne rozpatrywanego problemu otrzymuje się poprzez złożenie rozwiązań cząstkowych dla poszczególnych podobszarów – elementów skończonych. Dzięki takiemu podejściu MES pozwala na modelowanie systemów od dużej złożoności geometrycznej, niejednorodnym rozkładzie właściwości materiałowych, wchodzących w skomplikowane interakcje z otoczeniem.
Jednym z celów badawczych Międzyzakładowej Pracowni Modelowania Komputerowego jest utworzenie i rozwój modeli numerycznych tkanek roślinnych dla różnych skali przestrzennych.
Modelowanie właściwości mechanicznych tkanek roślinnych
Właściwości fizyczne materiałów roślinnych są wypadkową wielu czynników występujących w mikro i nano-skali, jak choćby mikrostruktury tkanki, ciśnienia wewnątrzkomórkowego, właściwości mechanicznych ścian komórkowych oraz właściwości blaszki środkowej. Analiza eksperymentalna tych czynników w odniesieniu do właściwości makroskopowych tkanki jest obecnie bardzo trudna ze względu na brak odpowiednich metod badawczych. Drogą do wyjaśnienia, jakie zjawiska i cechy budowy leżą u podstaw właściwości mechanicznych tkanek roślinnych są badania modelowe polegające na opracowaniu matematycznych modeli opisujących ich deformację.
Dotychczas większość znanych z literatury modeli tkanek roślinnych opierała się na zasadach klasycznej mechaniki ośrodka ciągłego. Najczęściej miały one charakter empiryczny lub analityczny, a ich parametry wyznaczane były na podstawie danych eksperymentalnych, uzyskanych w klasycznych próbach wytrzymałościowych. Modele oparte na tych założeniach, dzięki swojej prostocie znalazły zastosowanie w aplikacjach inżynierskich, jednakże nie pozwoliły na poznanie charakteru i przebiegu zjawisk leżących u podstaw mechanizmu uszkodzenia tkanek roślinnych.
Badania finansowane były w ramach projektu nr 2011/01/N/NZ9/02496 Narodowego Centrum Nauki.
Modelowanie struktury tkanki
Jednym z kroków poprzedzających właściwą analizę MES jest utworzenie wirtualnej reprezentacji badanego obiektu. Wirtualny model zdefiniowany jest przez geometrię, właściwości materiałowe oraz warunki brzegowe reprezentujące oddziaływania zewnętrze oraz wewnętrzne. Istotne jest aby odwzorować modelowany system z możliwie największą dokładnością, przy jednoczesnym zachowaniu pewnych uroszczeń, umożliwiających przeprowadzenie obliczeń w rozsądnym czasie.
W badaniach wstępnych przetestowane zostały trzy różne metody parametryzacji struktury tkanki roślinnej (Pieczywek et al., 2011). Wszystkie metody zastosować można do obrazów mikroskopowych uzyskanych przy użyciu laserowego mikroskopu konfokalnego (CLSM), aby następnie utworzyć na ich podstawie wirtualne modele numeryczne struktur komórkowych. Testom poddano metodę wektoryzacji, teselacji eliptycznej, oraz teselacji Woronoja. Jako materiał badawczy wybrane zostały tkanki parenchymatyczne ziemniaka oraz marchwi.
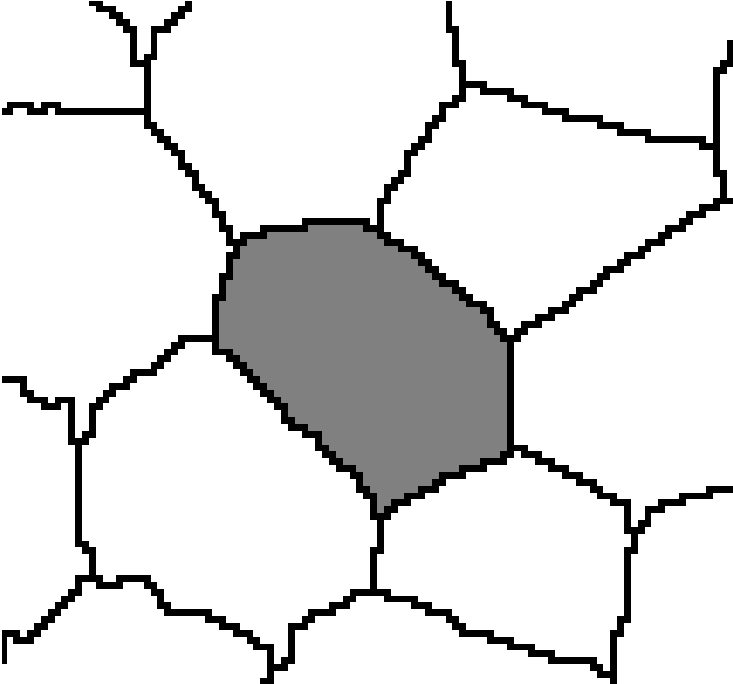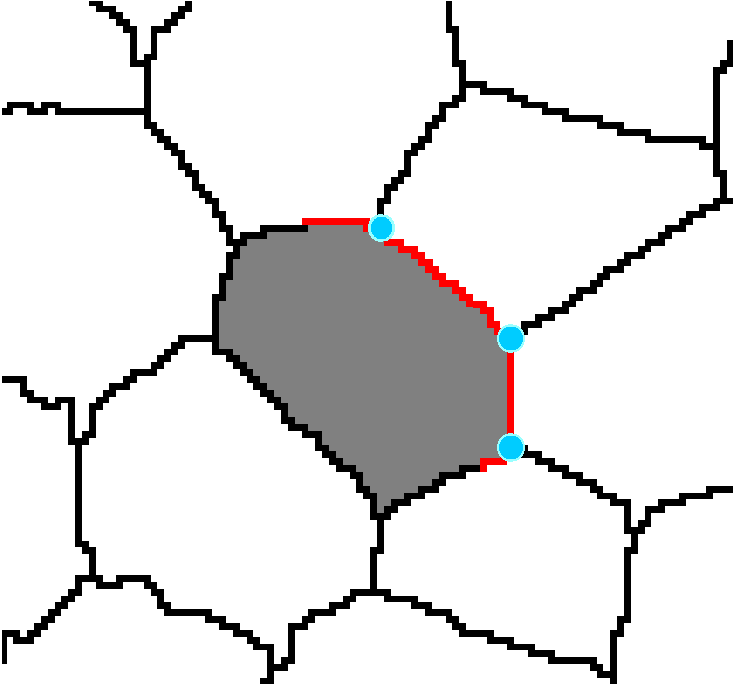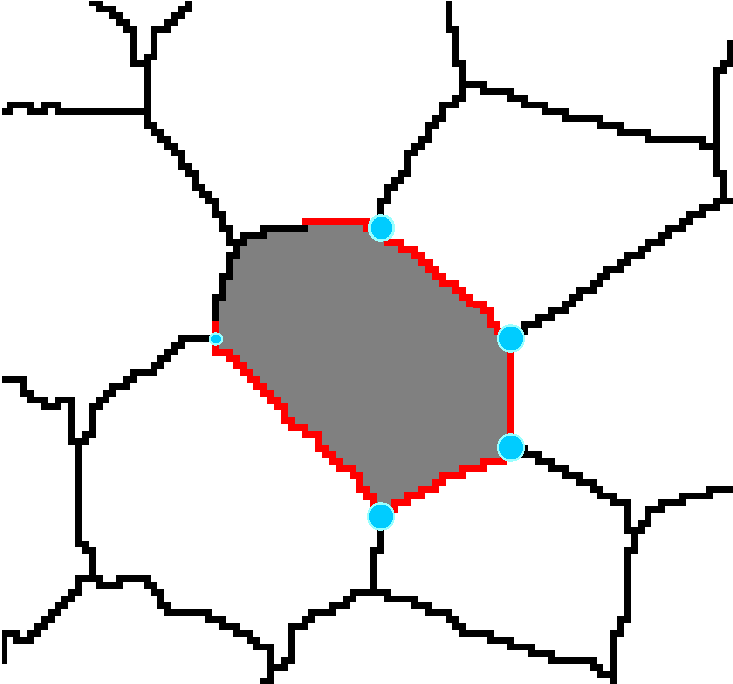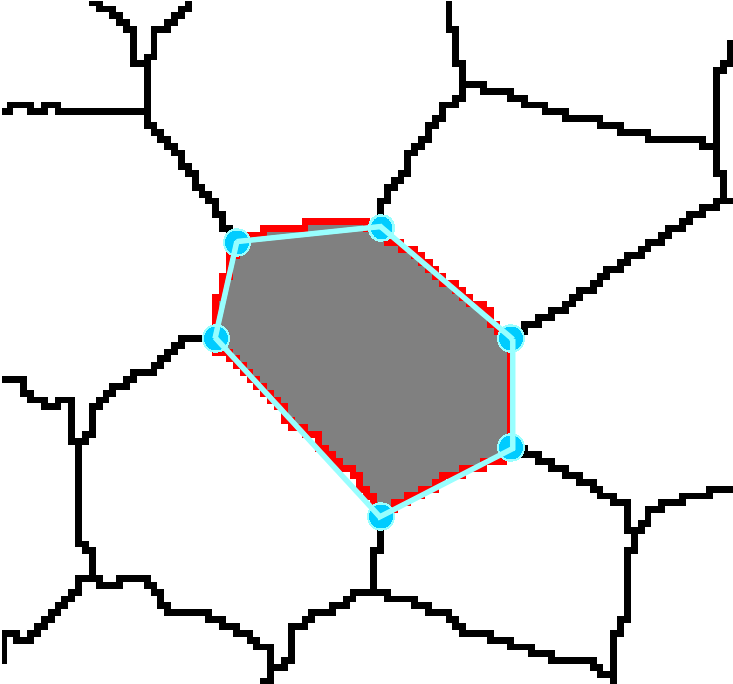
Rys. 1. Procedura wektoryzacji: detekcja krawędzi przekroju komórki, detekcja punktów przecięcia sąsiednich ścian komórkowych, łączenie punktów węzłowych w celu utworzenia wirtualnej komórki.
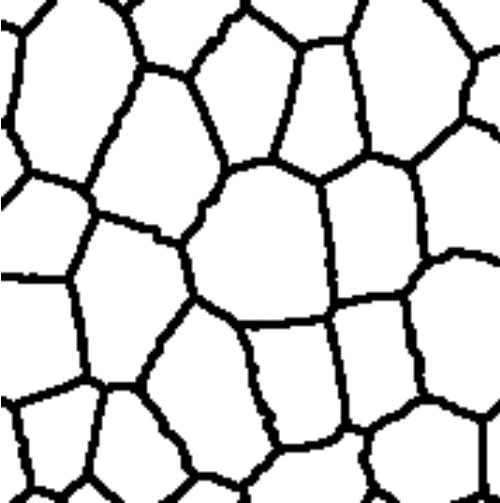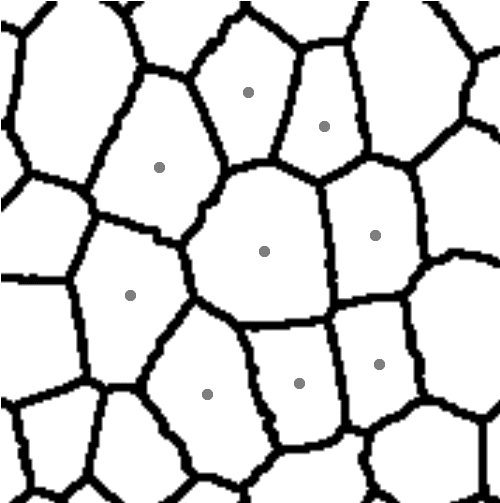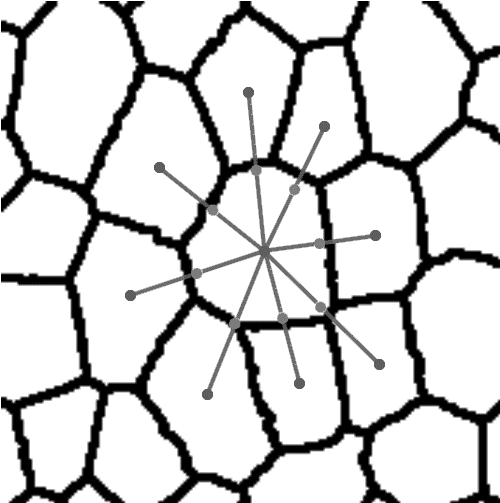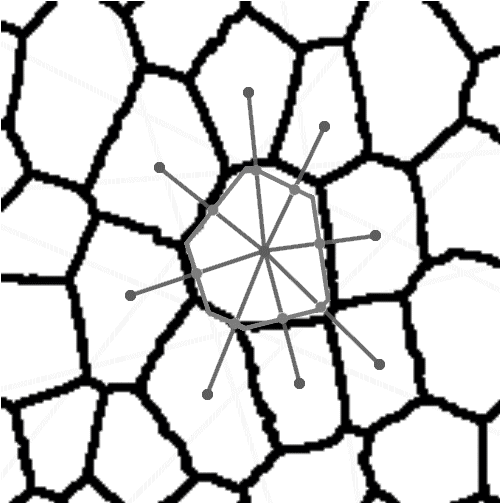
Rys. 2. Proces modelowania struktury tkanki na bazie algorytmu teselacji Woronoja.
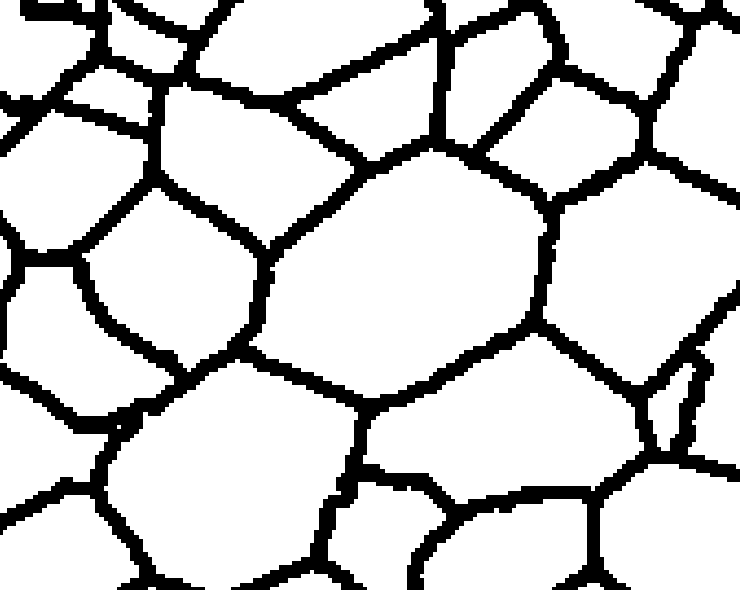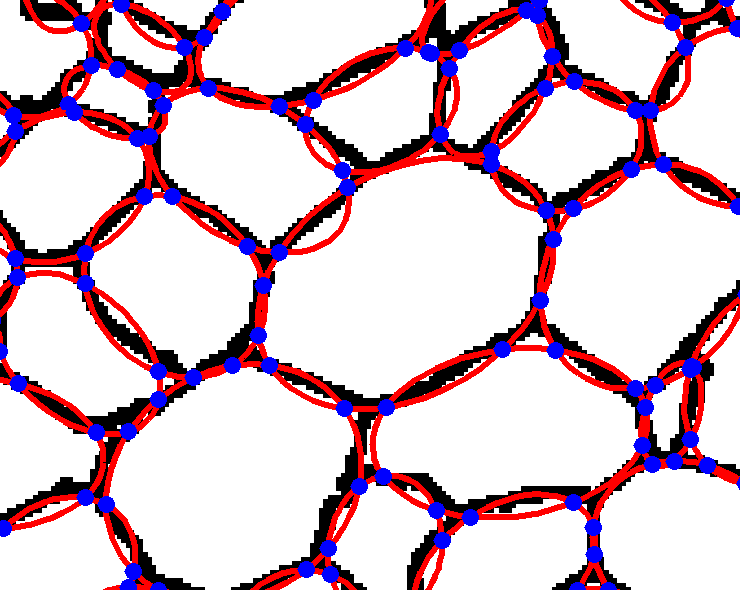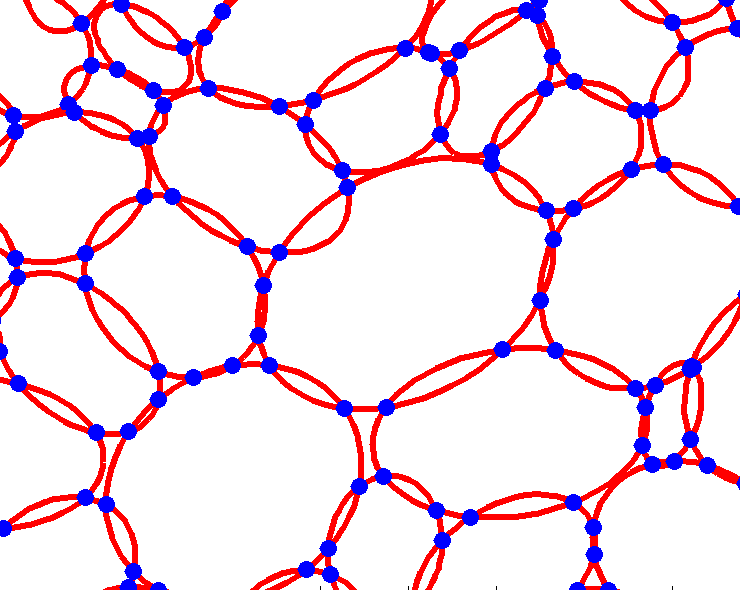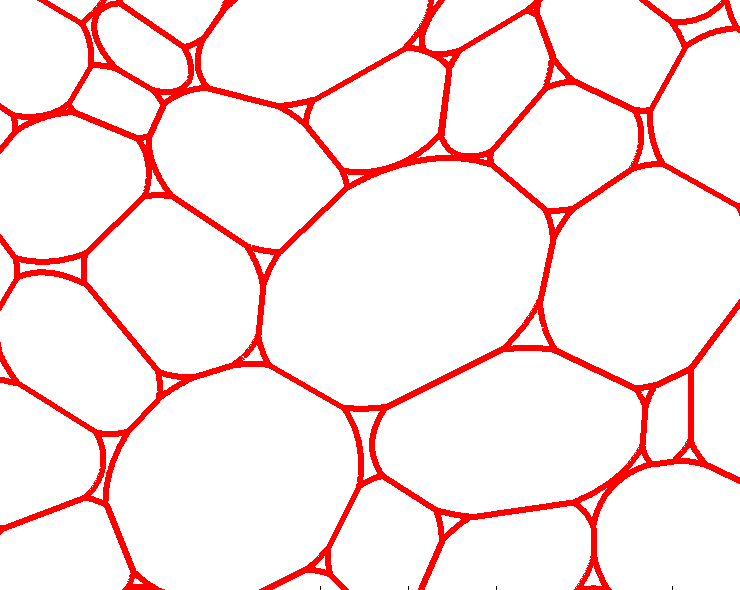
Rys. 3. Procedura teselacji eliptycznej: dopasowanie elips do obrysów komórek, wyznaczanie punktów przecięcia sąsiadujących elips, „obcięcie” pokrywających się części elips.
Dla wszystkich modeli geometrycznych wyznaczone zostały rozkłady statystyczne pięciu parametrów opisujących kształty komórek: pole powierzchni, obwód, orientacja, wydłużenie oraz współczynnik lokalnego powiązania (local indicator of spatial association) charakteryzujący przestrzenny rozkład wielkości komórek. Jakość odwzorowania struktury tkanki oceniona została na podstawie porównania rozkładów statystycznych parametrów geometrycznych komórek z obrazów mikroskopowych oraz ich wirtualnych model.
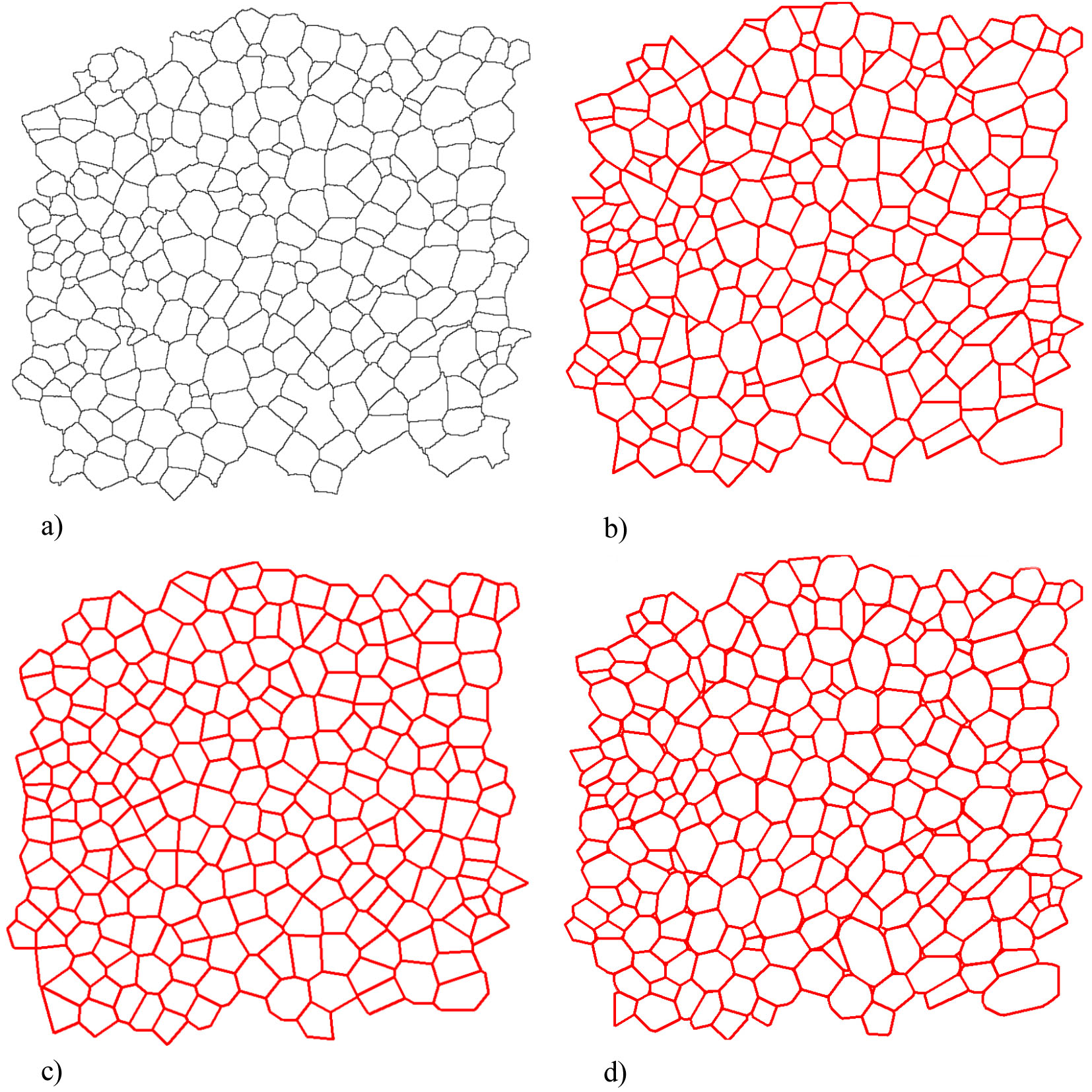
Rys. 4. Przykłady zastosowania metod parametryzacji do odwzorowania relatywnie jednorodnych struktur, a) przetworzony obraz mikroskopowy parenchymy ziemniaka, b) wektoryzacja, c) teselacja Woronoja, d) teselacja eliptyczna wykonana na obrazie bazowym.

Rys. 5. Przykłady zastosowania metod parametryzacji do odwzorowania nieregularnych struktur, a) przetworzony obraz mikroskopowy parenchymy ziemniaka, b) wektoryzacja, c) teselacja Woronoja, d) teselacja eliptyczna wykonana na obrazie bazowym.
Na bazie uzyskanych wyników stwierdzono, że teselacja Woronoja nie pozwala na uzyskanie statystycznie reprezentatywnych struktur komórkowych. Metoda wektoryzacji pozwalała na odwzorowanie ogólnego obrysu przekroju komórki, z zaniedbaniem krzywizny ścian komórkowych. Dla obu tych metod wirtualne komórki posiadały formę wielokątów oraz ściśle wypełniały przestrzeń, nie pozostawiając żadnych wolnych przestrzeni. Najlepszą jakość odwzorowania uzyskano przy użyciu teselacji eliptycznej. Modele uzyskane tą metodą uznać można za statystynie reprezentatywne odwzorowania realnych tkanek pod względem zachowania rozmiarów, kształtów jak i przestrzennego rozmieszczenia komórek.
Mikroskalowy model epidermy cebuli
W toku badań przeprowadzonych w ramach projektu NCN 2011/01/N/NZ9/02496 utworzony został model pozwalający przewidzieć właściwości mechaniczne tkanki na podstawie cech mikrostruktury, tj. budowy komórkowej (Pieczywek et al., 2014).. Do tego celu wybrano metodę elementów skończonych, która pozwoliła na utworzenie modelu uwzględniającego realną strukturę komórkową tkanki. Model został opracowany i zweryfikowany eksperymentalnie dla tkanki epidermy cebuli, jako prostego jednowarstwowego układu komórek.

Rys. 6. Proces deformacji epidermy cebuli podczas próby jednoosiowego rozciągania.

Rys. 7. Animacja przedstawiająca proced deformacji wirtualnej tkanki podczas symulacji próby jednoosiowego rozciągania w środowisku obliczeniowym MES ANSYS 11.
Dzięki przeprowadzonym symulacjom i badaniom eksperymentalnym, które uwzględniały najważniejsze czynniki determinujące mechanikę tkanek roślinnych, stwierdzono że opracowany model jest przydatny do predykcji charakterystyki mechanicznej tkanki wynikającej z turgoru oraz z budowy struktury komórkowej. W szczególnym przypadku splazmolizowanej tkanki, na podstawie dopasowania modelu do danych eksperymentalnych, opracowany model pozwala również wyznaczyć moduł Younga ściany komórkowej w obszarze sprężystym i sprężysto-plastycznym. Model pozwala również na obserwację rozkładu naprężeń w ścianach komórkowych podczas deformacji, co umożliwia predykcję potencjalnych stref rozwoju pęknięć w tkance.
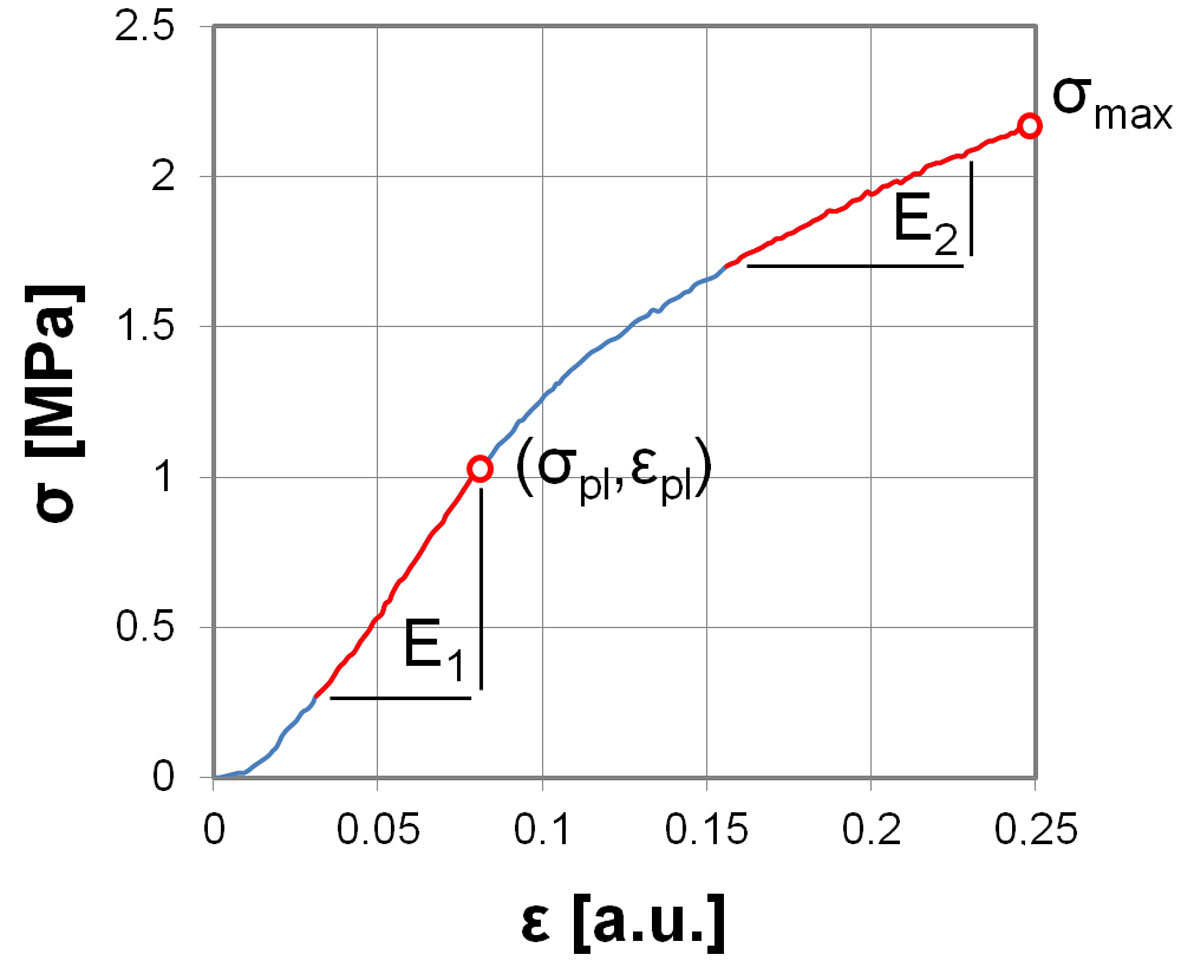
Rys. 8. Przykładowa charakterystyka naprężenia jako funkcji odkształcenia względnego, uzyskana w statycznej próbie jednoosiowego rozciągania tkanki roślinnej, z wyznaczanymi parametrami mechanicznymi – moduł sprężystości podłużnej E1, moduł umocnienia plastycznego E2, naprężenie oraz odkształcenie na granicy plastyczności σpl, εpl.
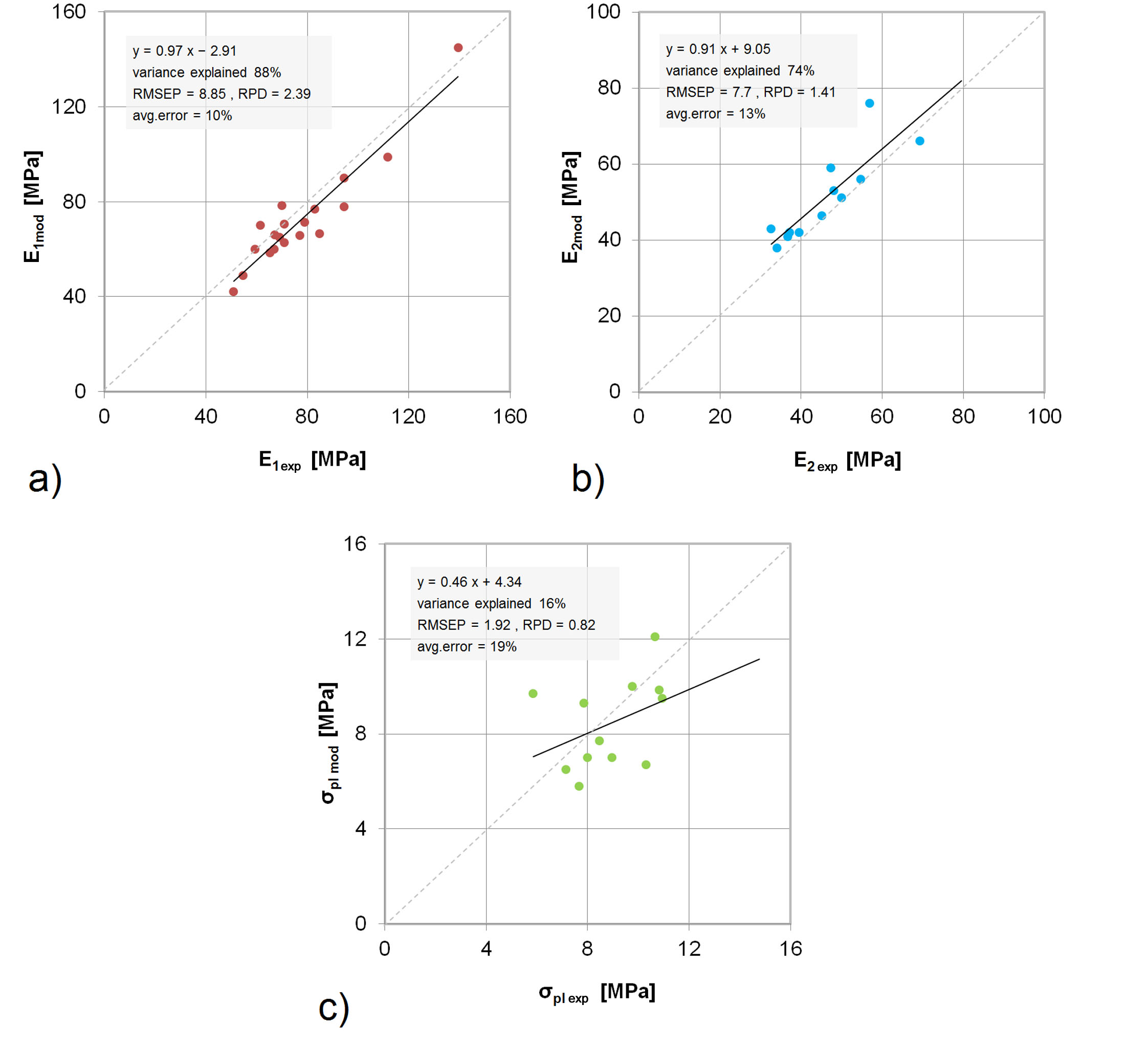
Rys. 9. Porównanie parametrów materiałowych wyznaczonych z testów mechanicznych z wynikami symulacji numerycznych
Opracowany model mechaniczny tkanki roślinnej, który uwzględnia realną heterogeniczną budowę komórkową, stanowi oryginalne rozwiązanie omawianego problemu naukowego. Mimo, że został opracowany na relatywnie prostej tkance epidermalnej, może zostać uogólniony do bardziej skomplikowanych tkanek miękiszowych o innym kształcie komórek oraz zawierających przestrzenie międzykomórkowe. Dzięki tym badaniom możliwe będzie nie tylko opracowanie doskonalszych i bardziej realnych modeli obliczeniowych do wyznaczania nieznanych parametrów mechanicznych tkanki roślinnej, ale również przyczyni się do zdobycia wiedzy pozwalającej kształtować wybrane parametry jakościowe owoców i warzyw, np. przez hodowlę odmian owoców, które ze względu na cechy morfologiczne tkanek byłyby odporniejsze na uszkodzenia lub byłyby opracowane pod kątem określonych preferencji konsumenta i przemysłu.
Dalsze prace rozwojowe
Symualcje automatycznie generowanych, w pełni tójwymiarowych struktur komórkowych.

